¿Cómo sé si mi modelo de predicción es realmente bueno?

Hace unas semanas, os contamos los distintos tipos de aprendizaje automático a través de una serie de ejemplos, y analizamos cómo elegir uno u otro en base a nuestros objetivos y a los conjuntos de datos disponibles para entrenar el algoritmo.

Ahora supongamos que contamos con un conjunto de datos ya etiquetado y que necesitamos entrenar un modelo de aprendizaje supervisado para resolver la tarea que nos ocupa. En este punto, necesitamos algún mecanismo que nos diga si el modelo ha aprendido correctamente o no. Eso es lo que vamos a tratar en este post, las métricas más utilizadas para evaluar la calidad de nuestros modelos.

La evaluación de modelos es un paso muy importante en la metodología de desarrollo de sistemas de aprendizaje automático. Ayuda a medir el rendimiento del modelo, es decir, cuantificar la calidad de las predicciones que ofrece. Para realizar este cometido utilizamos las métricas de evaluación, que dependen de la tarea de aprendizaje que apliquemos. Como vimos en el post anterior, dentro del aprendizaje supervisado existen dos tipos de tareas que difieren, principalmente, en el tipo de salida que ofrecen:

• Las tareas de clasificación, que producen como salida una etiqueta discreta, es decir, cuando la salida es una dentro de un conjunto finito.

• Las tareas de regresión, que producen como salida un valor real y continuo.

A continuación, te explicamos algunas de las métricas más utilizadas para evaluar el rendimiento de ambos tipos de tareas:

Evaluación de modelos de clasificación

Para poder entender mejor estas métricas, vamos a poner como ejemplo las predicciones de un modelo de clasificación para detectar enfermos de COVID. En la siguiente tabla podemos ver en la primera columna el identificador de ejemplo, en la segunda la clase que ha predicho el modelo, en la tercera la clase real y la cuarta columna indica si el modelo ha fallado en su predicción o no. En este caso, la clase positiva es “Si” y la clase negativa es “No”.

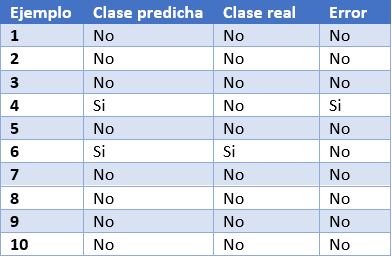
Algunos ejemplos de métricas de evaluación de modelos de clasificación son los siguientes:

• Matriz de confusión: es una herramienta ampliamente utilizada que permite inspeccionar y evaluar visualmente las predicciones de nuestro modelo. En cada fila se representa el número de predicciones de cada clase y en las columnas las instancias de la clase real.

La descripción de cada elemento de la matriz es la siguiente:

Verdadero positivo (VP): número de ejemplos positivos que el modelo predice como positivos. En el ejemplo que presentamos anteriormente, VP es 1 (del ejemplo 6).

Falso positivo (FP): número de ejemplos negativos que el modelo predice como positivos. En nuestro ejemplo, FP es igual a 1 (del ejemplo 4).

Falso negativo (FN): número de ejemplos positivos que el modelo predice como negativos. FN en el ejemplo sería 0.

Verdadero negativo (VN): número de ejemplos negativos que el modelo predice como negativos. En el ejemplo, VN es 8.

• Exactitud o accuracy: la fracción de predicciones que el modelo realizó correctamente.  Se representa como un porcentaje o un valor entre 0 y 1. Es una buena métrica cuando tenemos un conjunto de datos balanceado, esto es, cuando el número de etiquetas de cada clase es similar. La exactitud de nuestro modelo de ejemplo es de 0.9, ya que ha acertado 9 predicciones de 10.  Si nuestro modelo hubiese predicho siempre la etiqueta “No”, la exactitud sería de igualmente de 0.9, pero no resuelve nuestro problema de identificar enfermos de COVID.
• Recall o sensibilidad: indica la proporción de ejemplos positivos que están identificados correctamente por el modelo entre todos los positivos reales. Es decir, VP / (VP + FN). En nuestro ejemplo, el valor de sensibilidad sería 1 / (1 + 0) = 1. Si evaluásemos con esta métrica un modelo que siempre prediga la etiqueta positiva (“Si”) tendría una sensibilidad de 1, pero no sería un modelo demasiado inteligente. Aunque lo ideal para nuestro modelo de detección de COVID es maximizar la sensibilidad, esta métrica por sí sola no nos asegura que tengamos un buen modelo.
• Precision: esta métrica está determinada por la fracción de elementos clasificados correctamente como positivo entre todos los que el modelo ha clasificado como positivos. La fórmula es VP / (VP + FP). El modelo de ejemplo tendría una precisión de 1 / (1 + 1) = 0.5. Volvamos ahora al modelo que siempre predice la etiqueta positiva. En ese caso, la precisión del modelo es 1 / (1 + 9) = 0.1. Vemos como este modelo tenía una sensibilidad máxima, pero tiene una precisión muy pobre. En este caso necesitamos de las dos métricas para evaluar la calidad real del modelo.
• F1 score: combina las métricas Precision y Recall para dar un único resultado. Esta métrica es la más apropiada cuando tenemos conjuntos de datos no balanceados. Se calcula como la media armónica de Precision y Recal. La fórmula es F1 = (2 * precision * recall) / (precision + recall). Quizá te preguntes por qué la media armónica y no la simple. Esto es porque la media armónica hace que si una de las dos medidas es pequeña (aunque la otra sea máxima), el valor de F1 score va a ser pequeño.

Evaluación de modelos de regresión

A diferencia de los modelos de clasificación, en los modelos de regresión es casi imposible predecir el valor exacto, sino que más bien se busca estar lo más cerca posible del valor real, por lo que la mayoría de las métricas, con sutiles diferencias entre ellas, van a centrarse en medir eso: lo cerca (o lejos) que están las predicciones de los valores reales.

En este caso, tenemos como ejemplo las predicciones de un modelo que determina el precio de relojes dependiendo de sus características. En la tabla mostramos el precio predicho por el modelo, el precio real, el error absoluto y el error elevado al cuadrado.

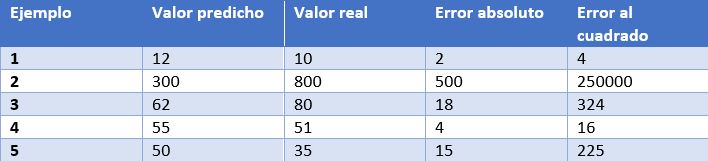
Algunas de las métricas de evaluación más comunes para los modelos de regresión son:

• Error medio absoluto: Es la media de las diferencias absolutas entre el valor objetivo y el predicho. Al no elevar al cuadrado, no penaliza los errores grandes, lo que la hace no muy sensible a valores anómalos, por lo que no es una métrica recomendable en modelos en los que se deba prestar atención a éstos. Esta métrica también representa el error en la misma escala que los valores reales. Lo más deseable es que su valor sea cercano a cero. Para nuestro modelo de cálculo de precios de relojes, el error medio absoluto es 107.8.
• Media de los errores al cuadrado (error cuadrático medio): Una de las medidas más utilizadas en tareas de regresión. Es simplemente la media de las diferencias entre el valor objetivo y el predicho al cuadrado. Al elevar al cuadrado los errores, magnifica los errores grandes, por lo que hay que utilizarla con cuidado cuando tenemos valores anómalos en nuestro conjunto de datos. Puede tomar valores entre 0 e infinito. Cuanto más cerca de cero esté la métrica, mejor. El error cuadrático medio del modelo de ejemplo es 50113.8. Vemos como en el caso de nuestro ejemplo se magnifican los errores grandes.
• Raíz cuadrada de la media del error al cuadrado: Es igual a la raíz cuadrada de la métrica anterior. La ventaja de esta métrica es que presenta el error en las mismas unidades que la variable objetivo, lo que la hace más fácil de entender. Para nuestro modelo este error es igual a 223.86.
• R cuadrado: también llamado coeficiente de determinación. Esta métrica difiere de las anteriores, ya que compara nuestro modelo con un modelo básico que siempre devuelve como predicción la media de los valores objetivo de entrenamiento. La comparación entre estos dos modelos se realiza en base a la media de los errores al cuadrado de cada modelo. Los valores que puede tomar esta métrica van desde menos infinito a 1. Cuanto más cercano a 1 sea el valor de esta métrica, mejor será nuestro modelo. El valor de R cuadrado para el modelo será de 0.455.
• R cuadrado ajustado. Una mejora de R cuadrado. El problema de la métrica anterior es que cada vez que se añaden más variables independientes (o variables predictoras) al modelo, R cuadrado se queda igual o mejora, pero nunca empeora, lo que puede llegar a confundirnos, ya que, porque un modelo utilice más variables predictoras que otro, no quiere decir que sea mejor. R cuadrado ajustado compensa la adición de variables independientes. El valor de R cuadrado ajustado siempre va a ser menor o igual al de R cuadrado, pero esta métrica mostrará mejoría cuando el modelo sea realmente mejor. Para esta medida no podemos hacer el cálculo para nuestro modelo de ejemplo porque, como hemos visto antes, depende del número de ejemplos y el número de variables utilizadas para entrenar dicho modelo.

Conclusión

A la hora de trabajar con algoritmos de aprendizaje supervisado es muy importante la elección de una métrica de evaluación correcta para nuestro modelo. Para los modelos de clasificación es muy importante prestar atención al conjunto de datos y comprobar si es balanceado o no. En los modelos de regresión hay que considerar los valores anómalos y si queremos penalizar errores grandes o no.

No obstante, generalmente, el dominio de negocio será el que nos guíe en la correcta elección de la métrica. Para un modelo de detección de enfermedades, como el que hemos visto, nos interesa que tenga una alta sensibilidad, pero también nos interesa que tenga un buen valor de precisión, por lo que F1-score sería una opción inteligente. Por otro lado, en un modelo para predecir la demanda de un producto (y por lo tanto de producción), donde un exceso de stock puede incurrir en un sobrecoste por almacenamiento de mercancía, quizás sea una buena idea utilizar la media de los errores al cuadrado para penalizar los errores grandes.

Contenido elaborado por Jose Antonio Sanchez, experto en Ciencia de datos y entusiasta de la Inteligencia Artificial .

Los contenidos y los puntos de vista reflejados en esta publicación son responsabilidad exclusiva de su autor.